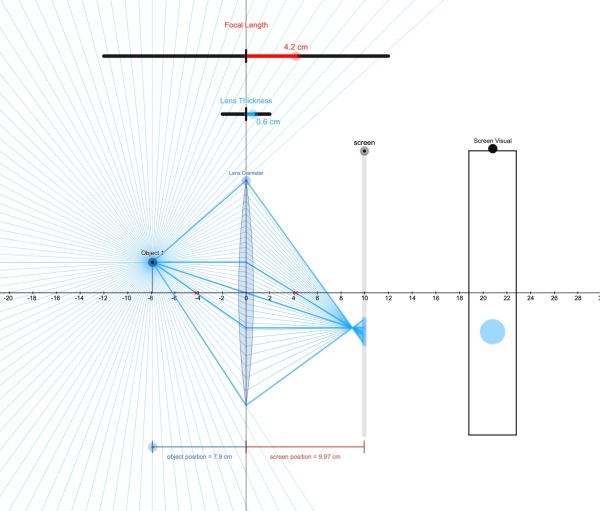
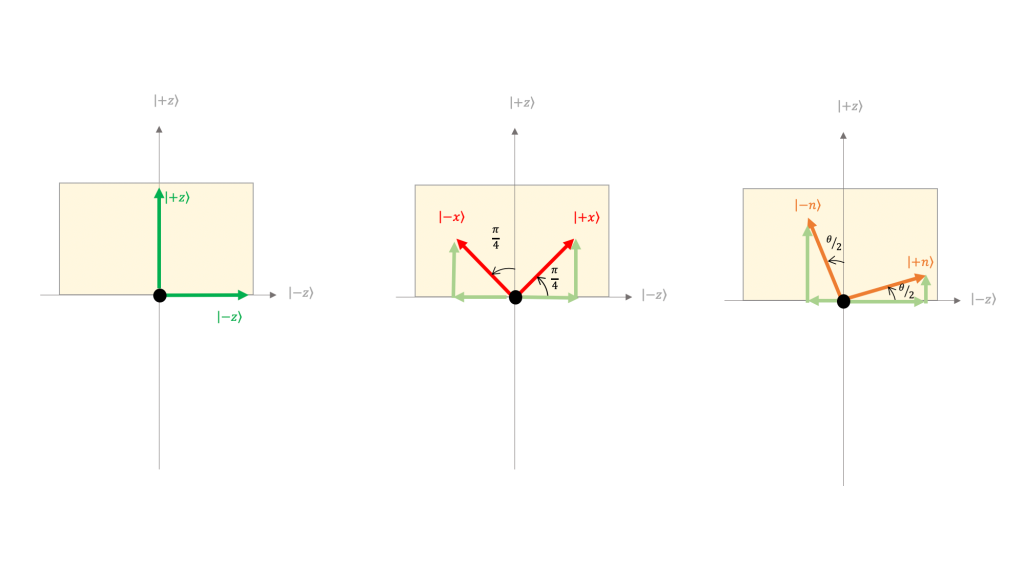
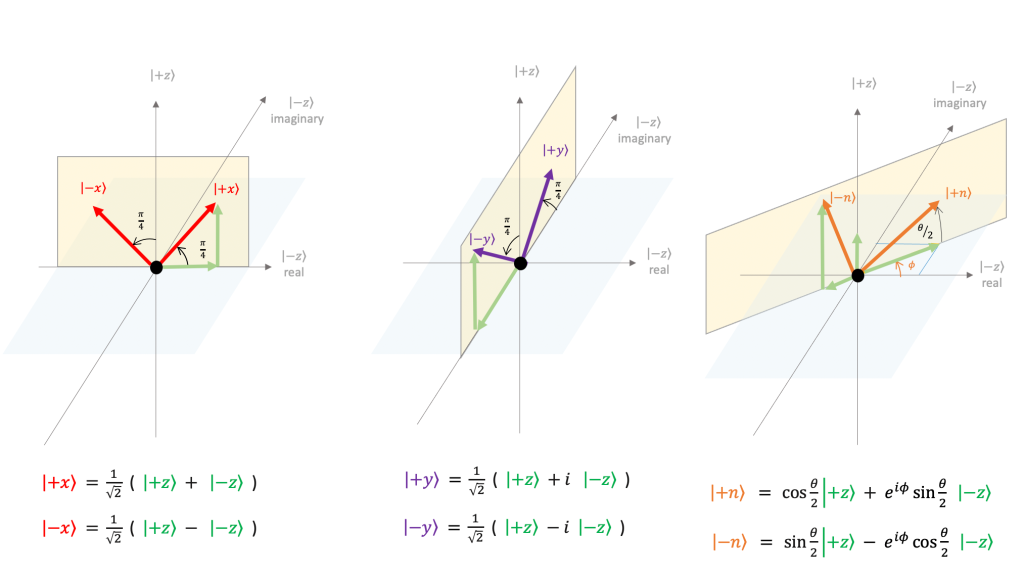
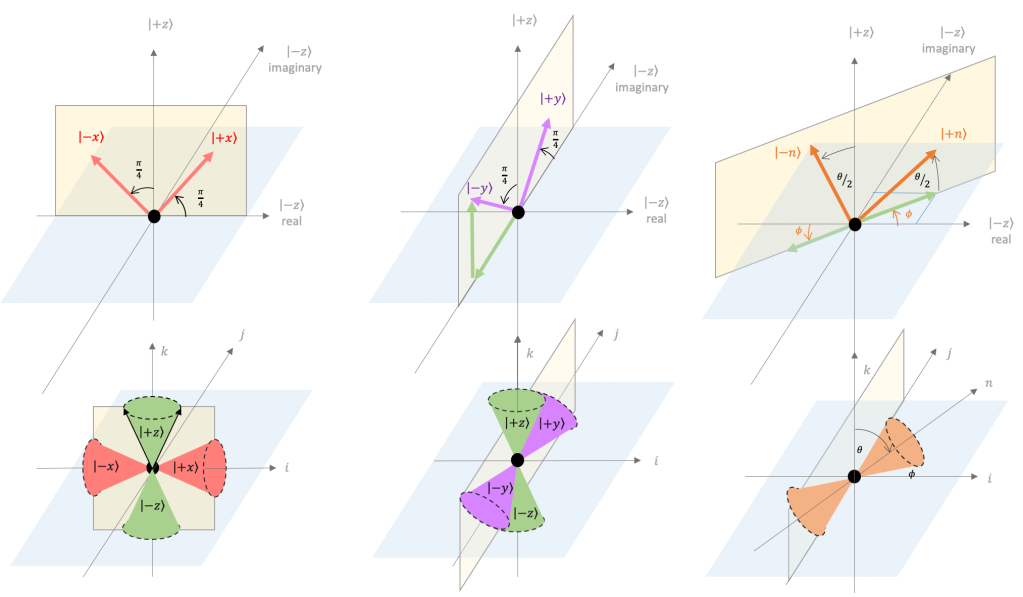
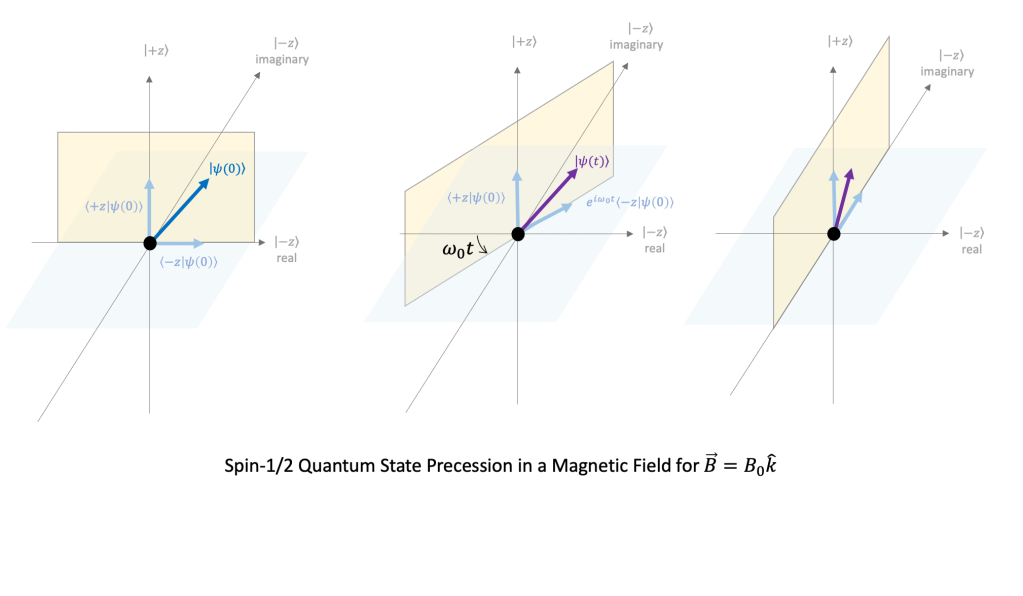
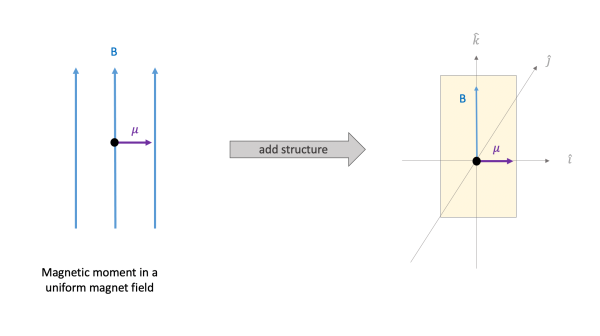
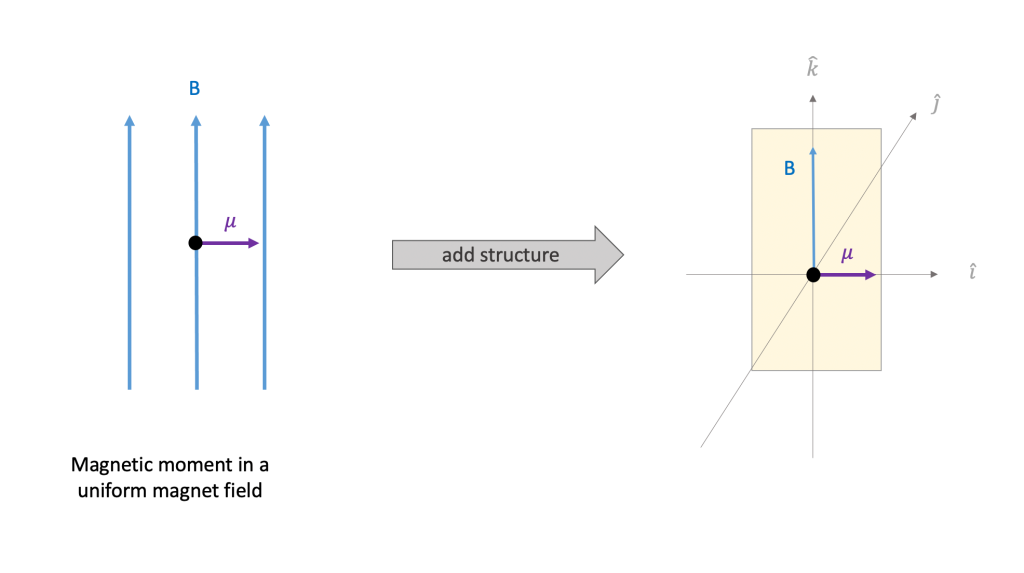
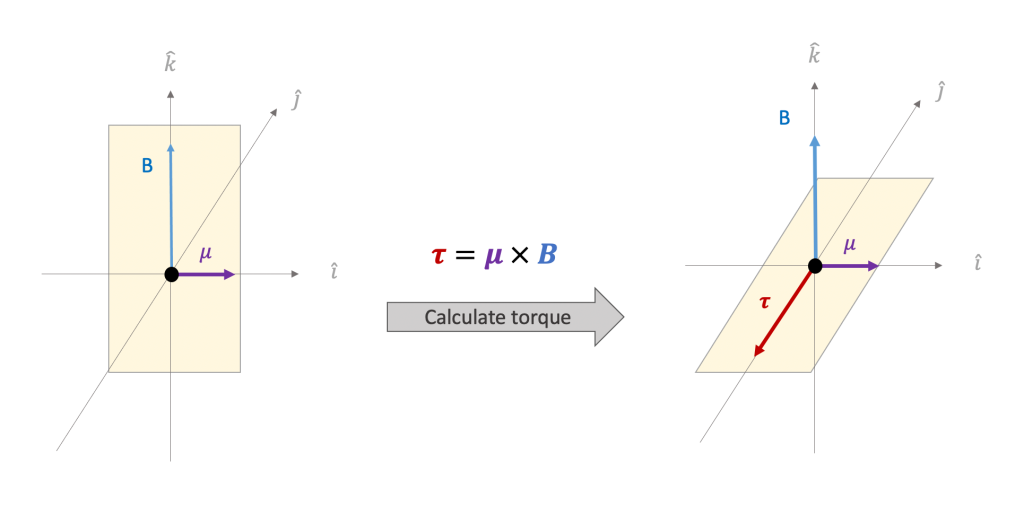
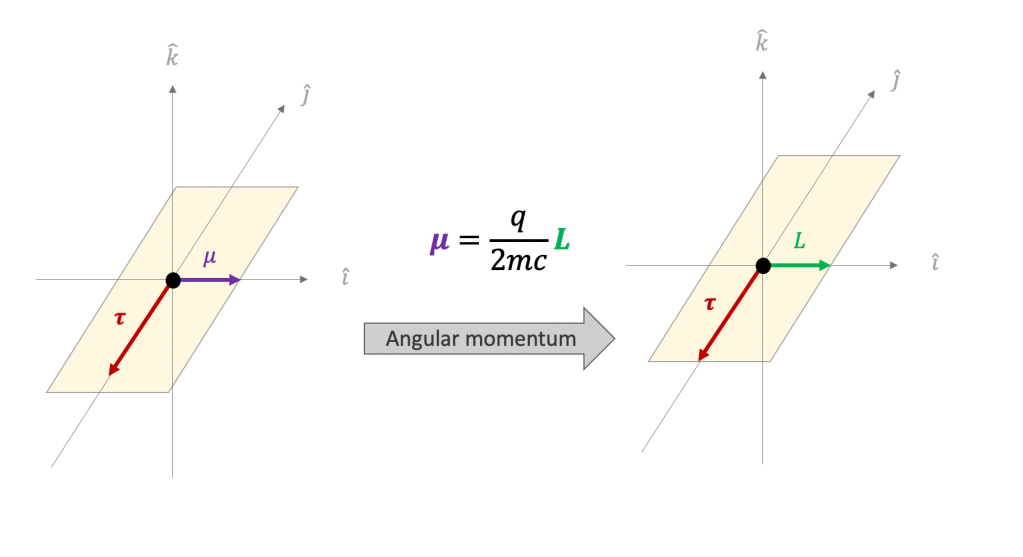
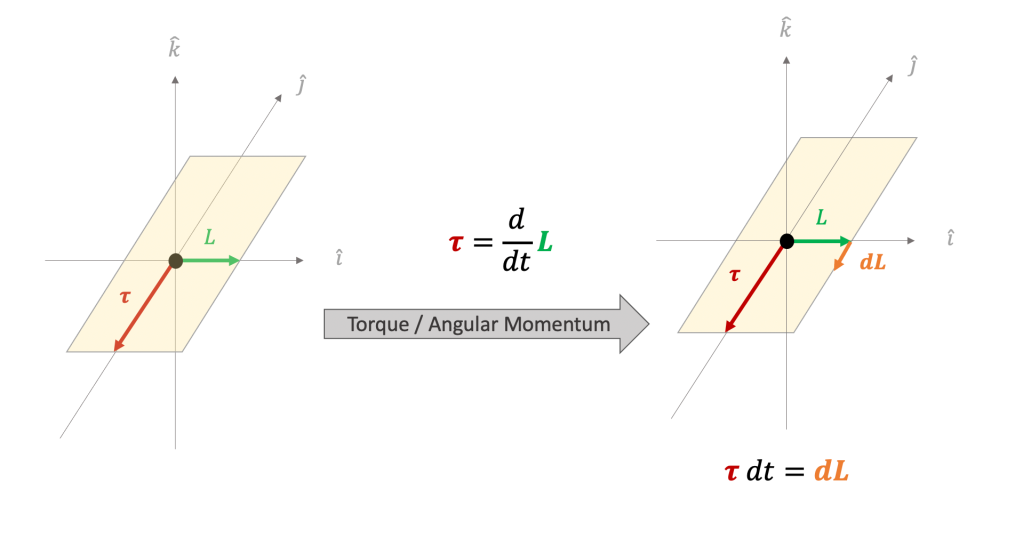
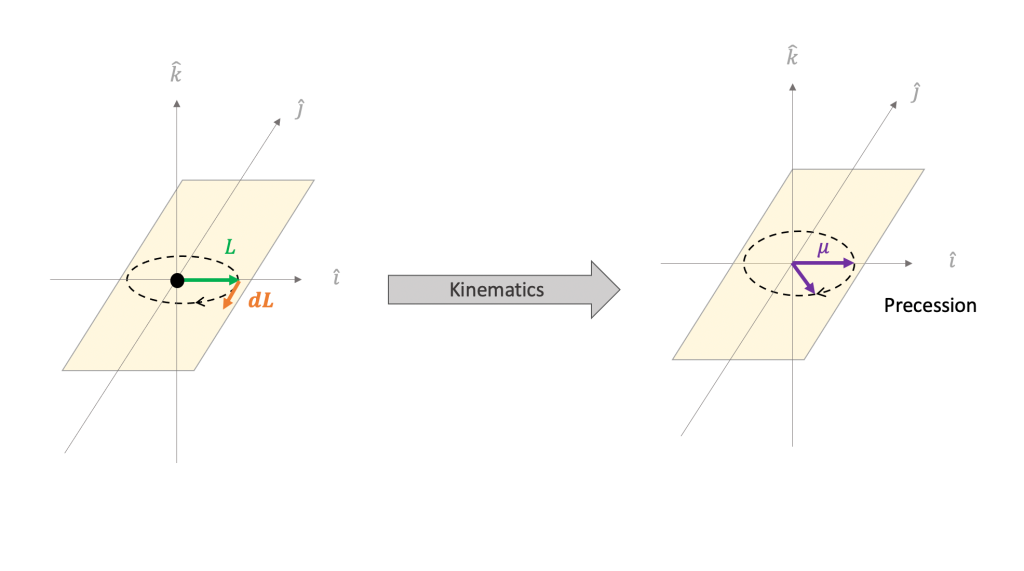
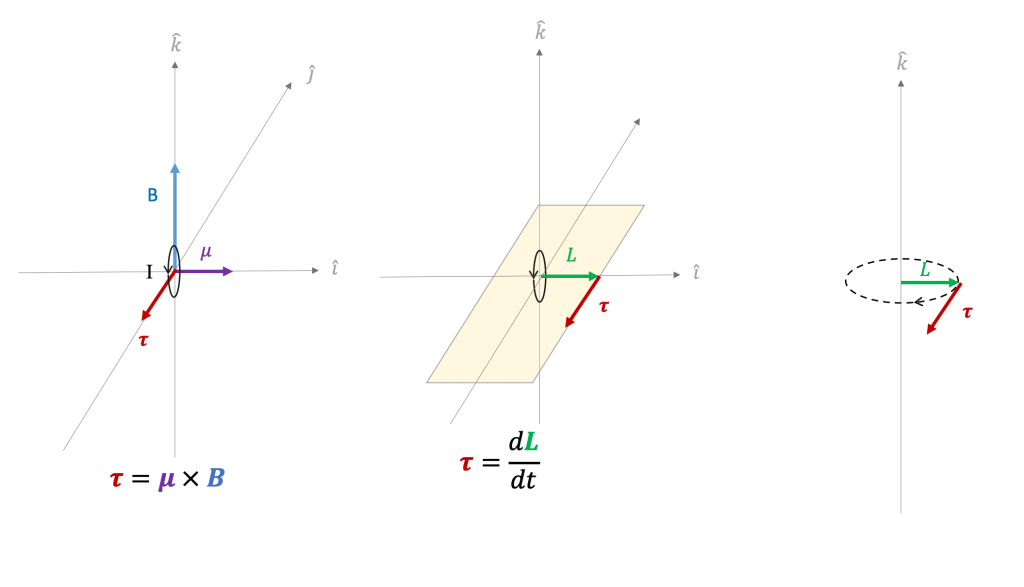
Goals for Spring 2021
1. Spend less time sitting. Standing desk!
2. Stay Better Hydrated.
3. Allocate and make good use of dedicated grading time slots in my weekly schedule.
4. Minimize the amount of time I spend working during non-work hours (evenings and weekends).
5. Continue with Physical Therapy and work toward getting back to regular exercise.
6. Use January to get courses organized and ready to be running efficiently, rather than tinkering to make improvements / adjustments.
7. Minimize zoom meetings. Use asynchronous collaboration more. Keep ending times for zoom meetings firm with time for breaks in between.
Bigger Challenge that I don’t know what to do about:
I will be course manager / organizer for 2nd semester algebra-based physics. Watching others in fall implement various assessment systems seemed miserable for everyone. I have a good sense of what I would do in my own independently run course, but a big collaborative course with many instructors is quite different. I don’t want to add workload, or too many changes, or additional stress to the instructors, but I also know I want to minimize the harm and stress to students. What the instructors did last semester seems both unsustainable and harmful, so I don’t think I can ethically just repeat what they did.
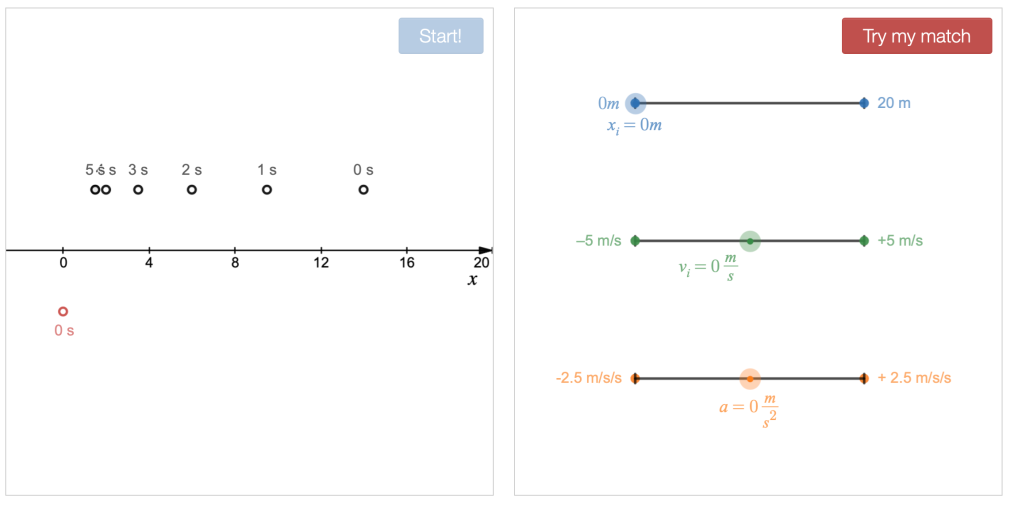
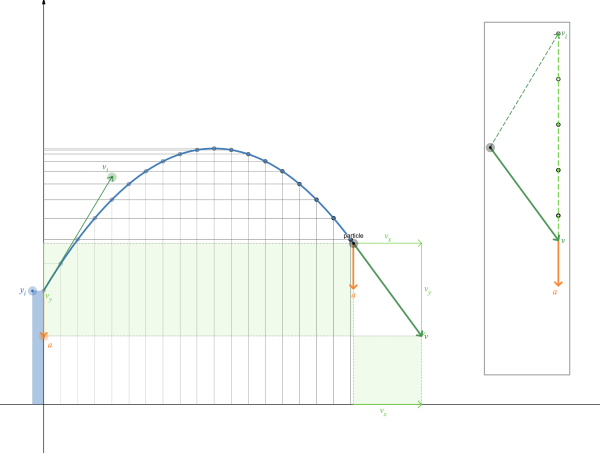
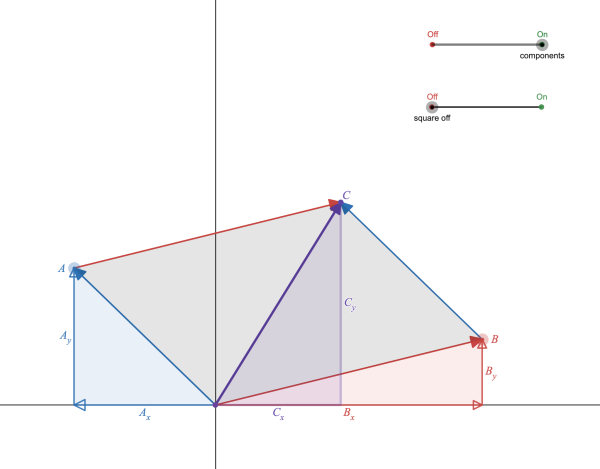
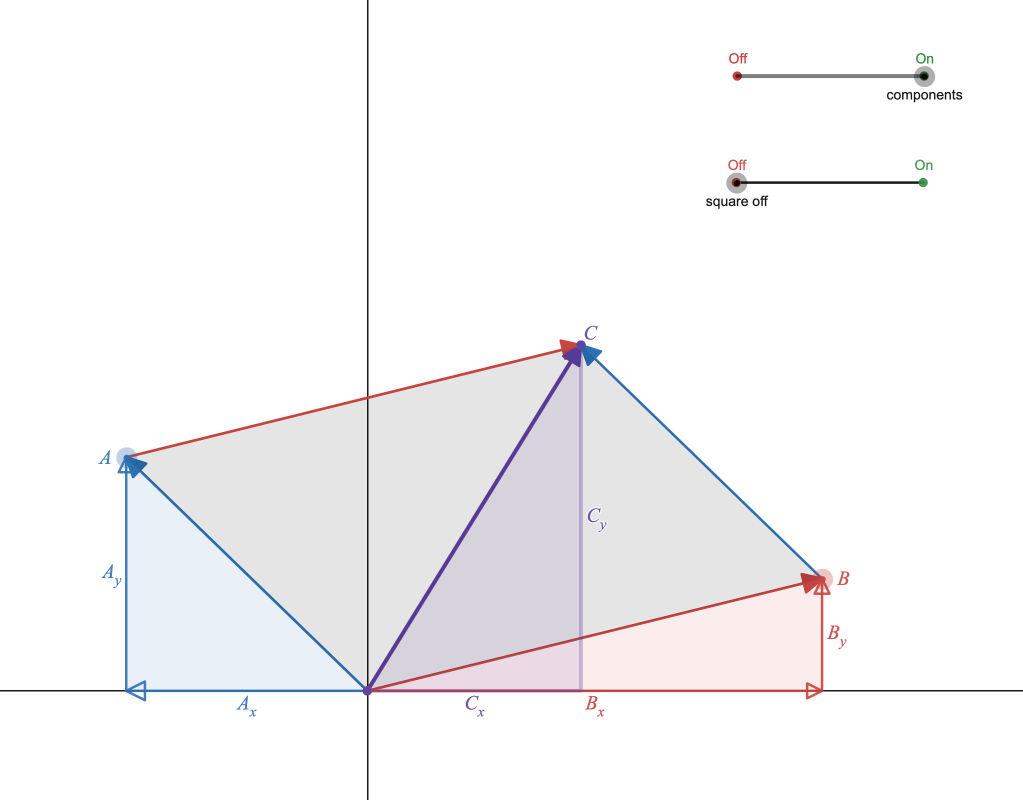
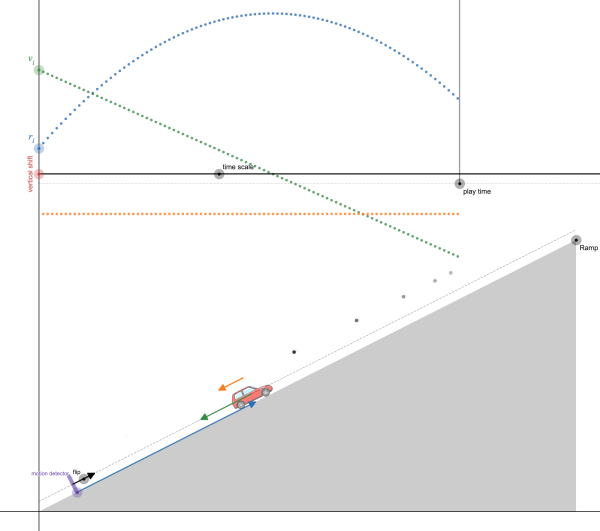
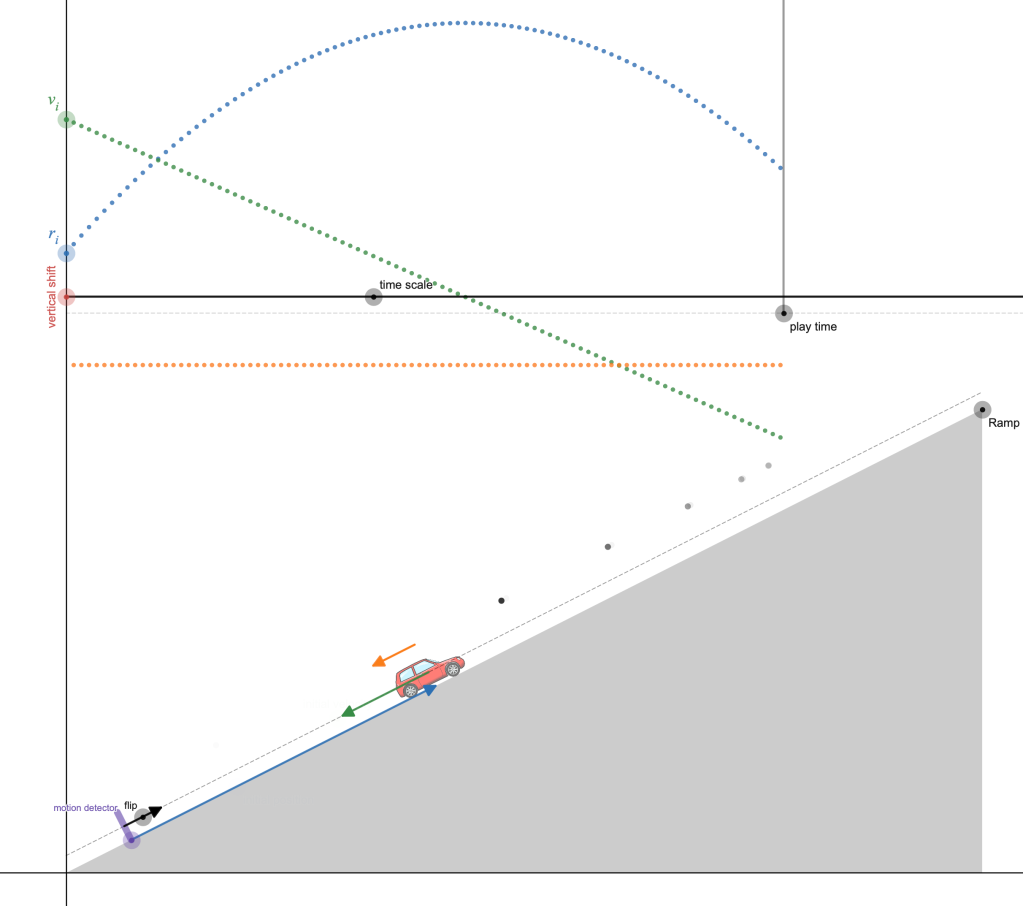
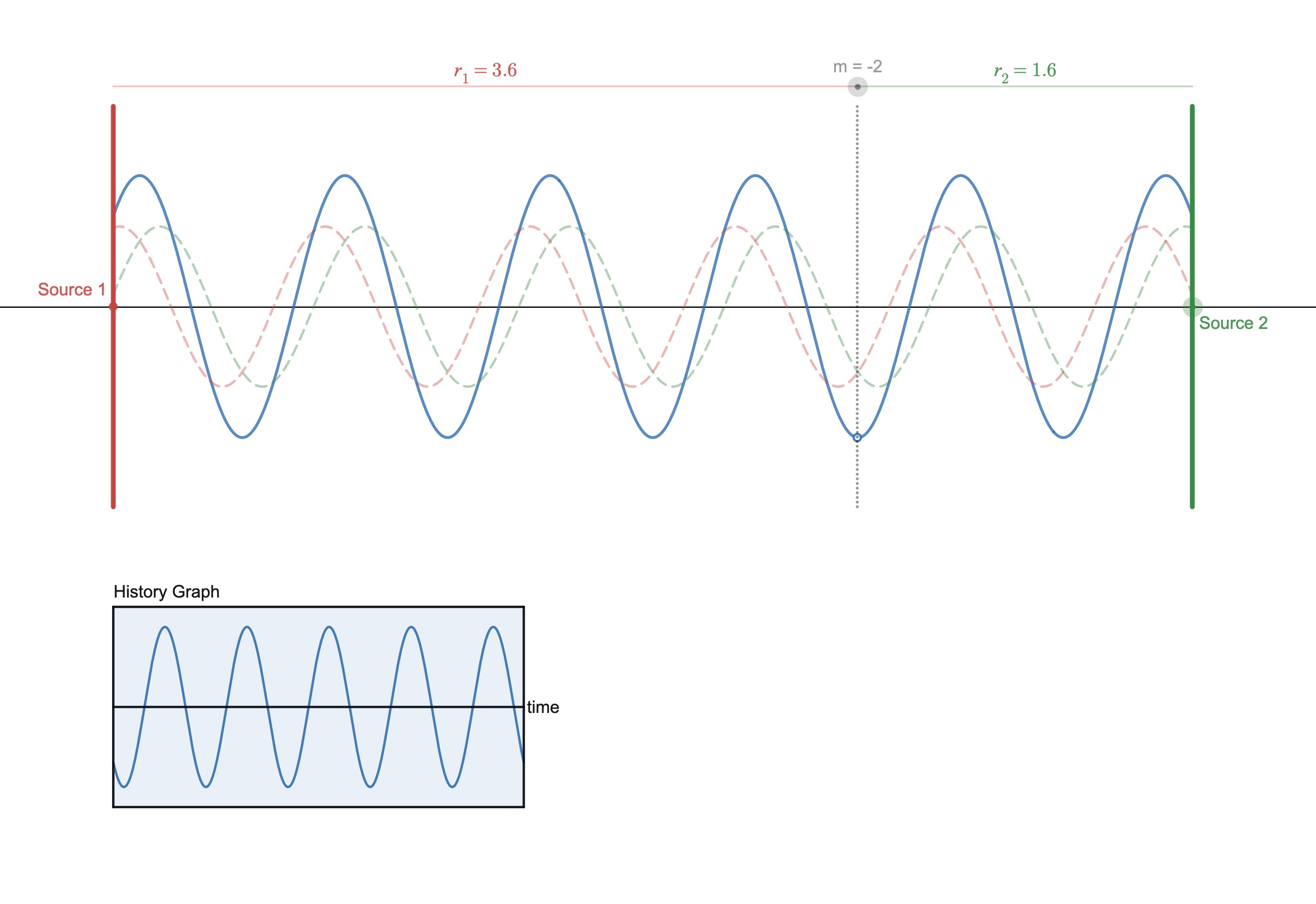
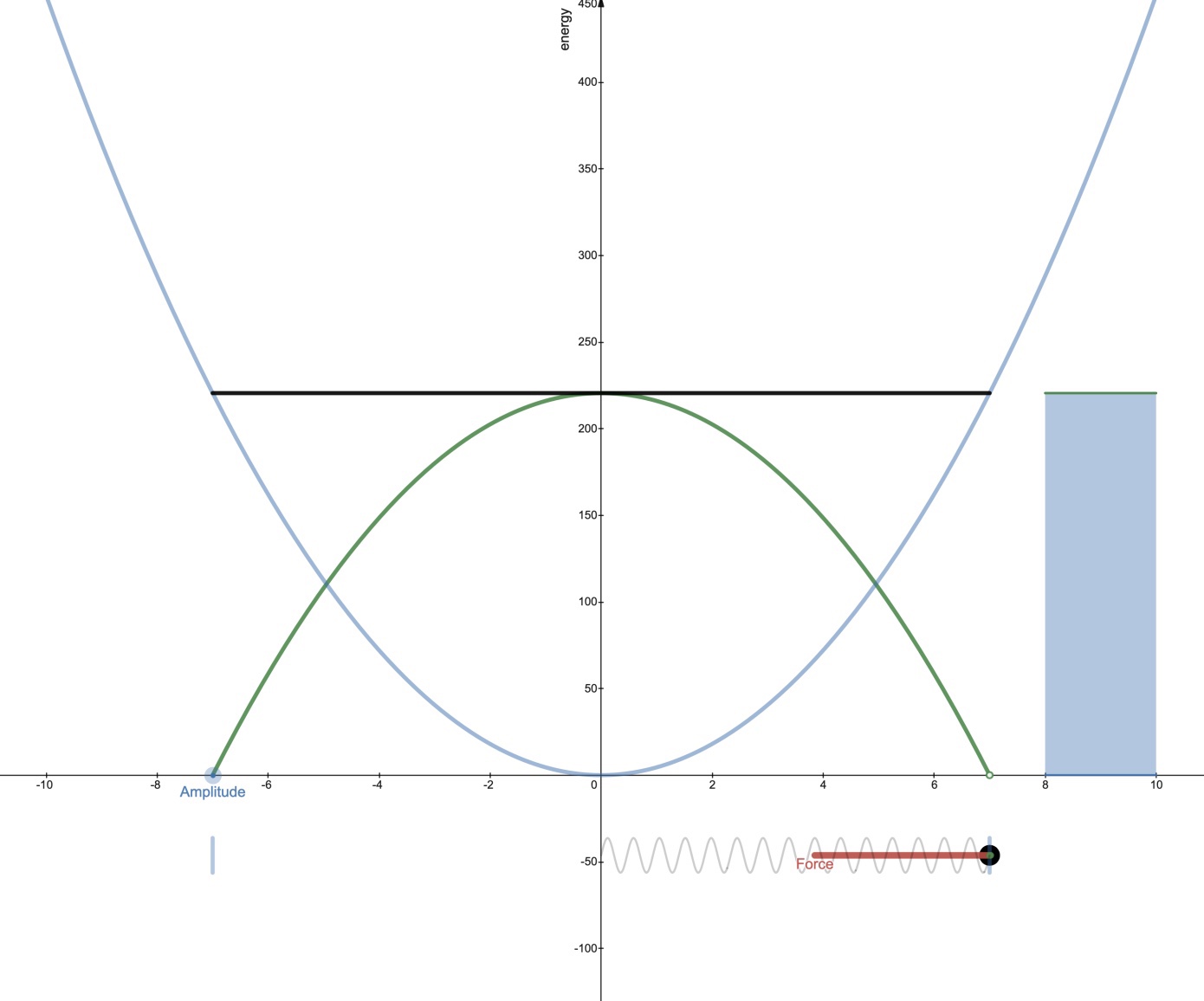
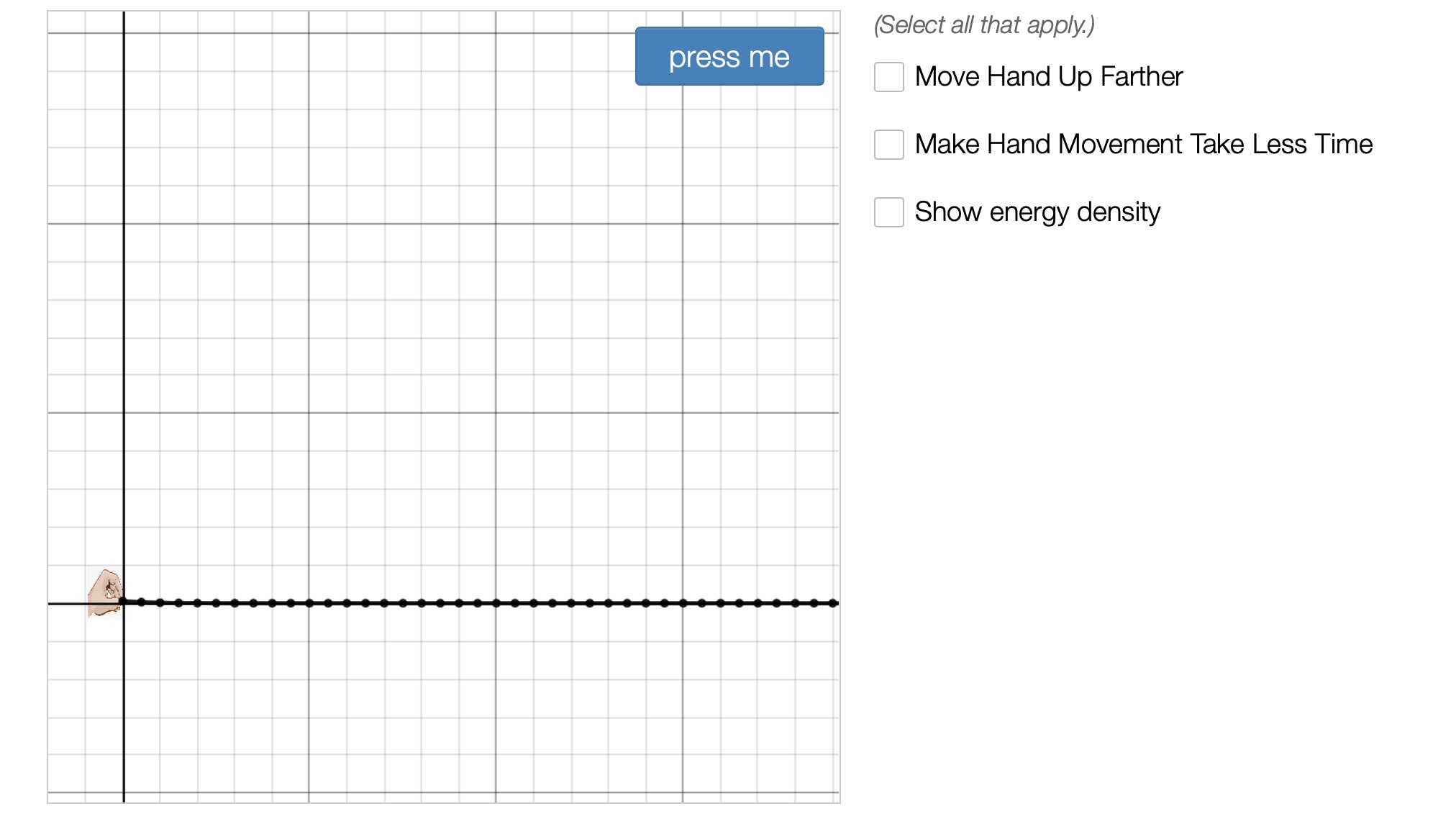
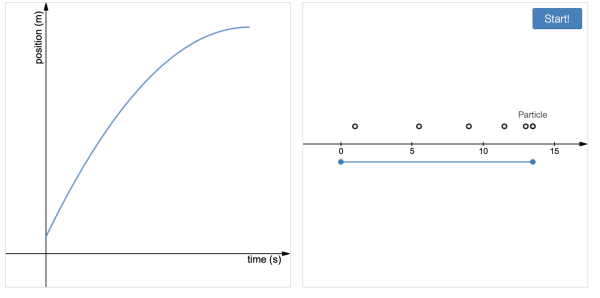
Live Animated Graphs and Motion Diagrams
Not really a student activity, but just an instructional resource that can be used as demonstrations or copied and pasted in desmos activity files you create.
https://teacher.desmos.com/activitybuilder/custom/5f554a089c56323f485e2f31
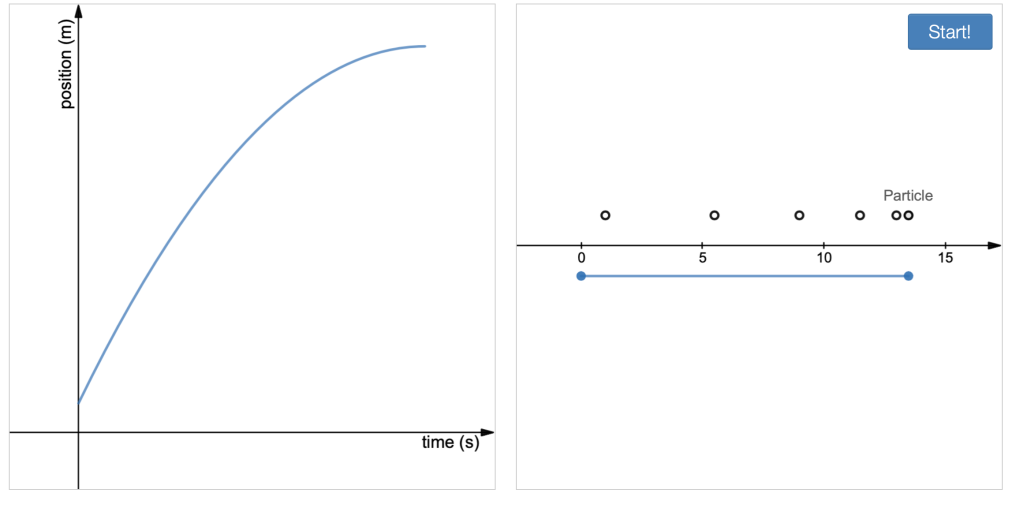
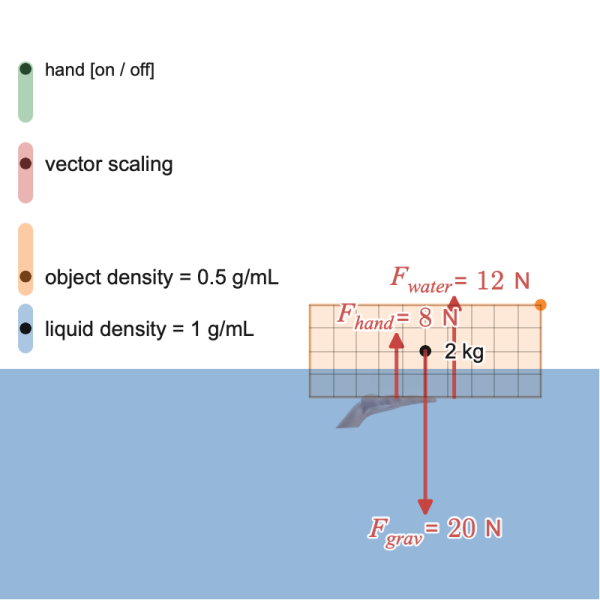
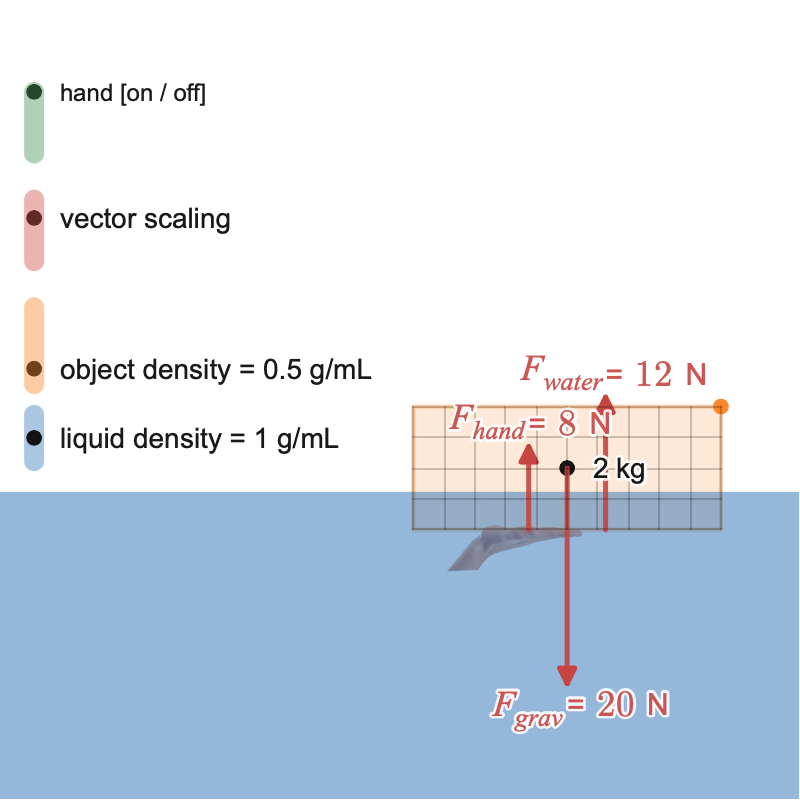
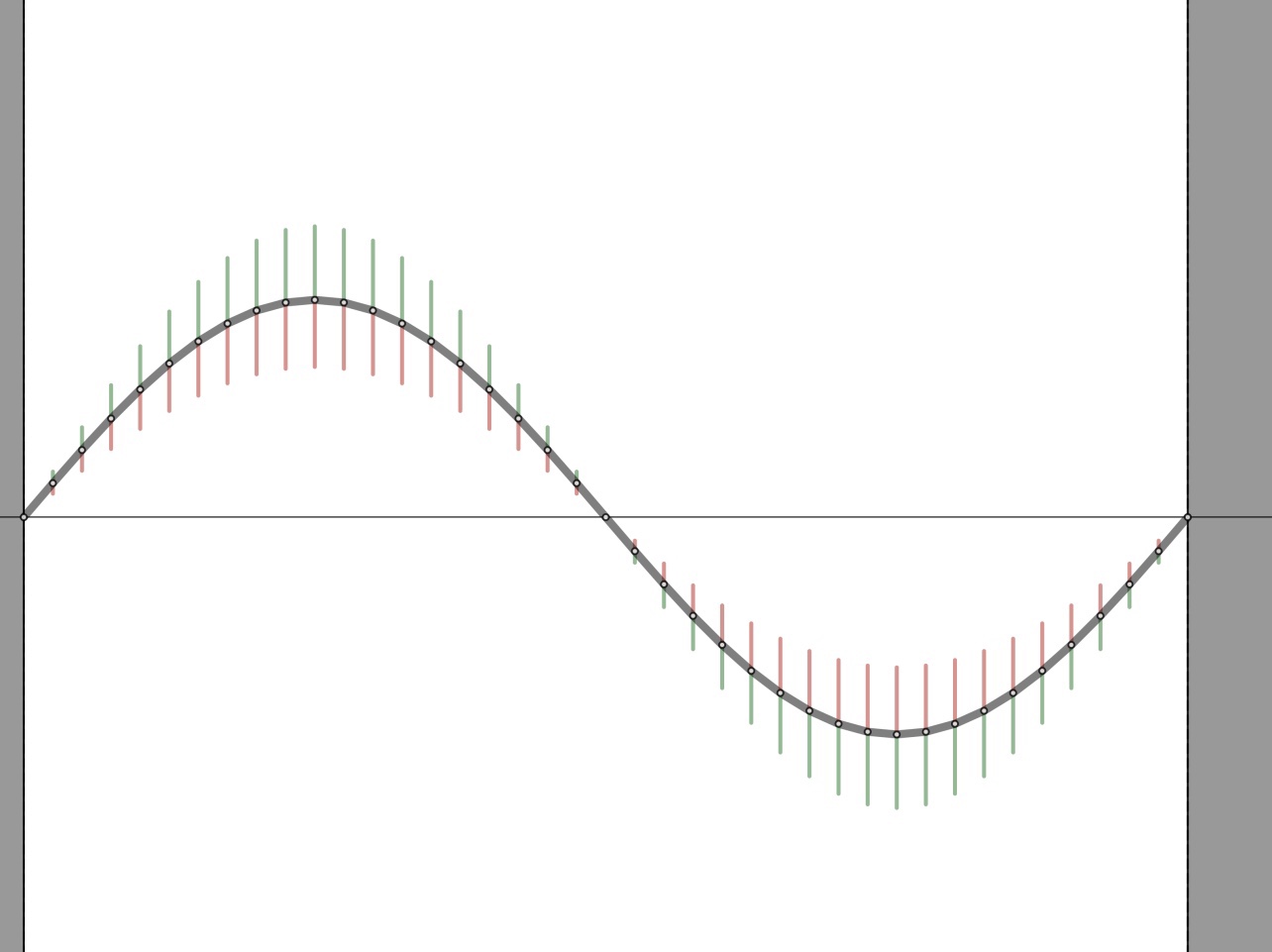
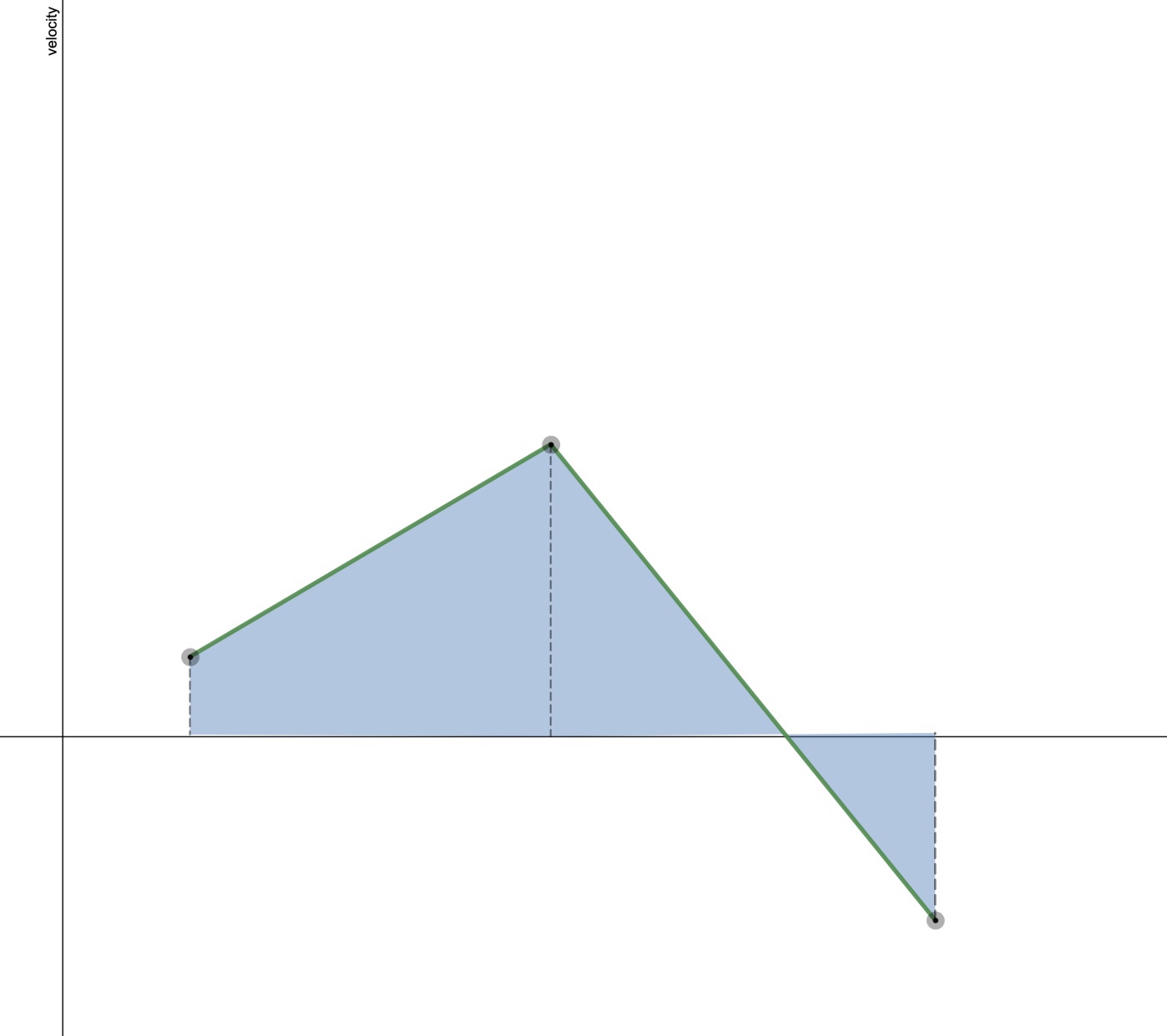
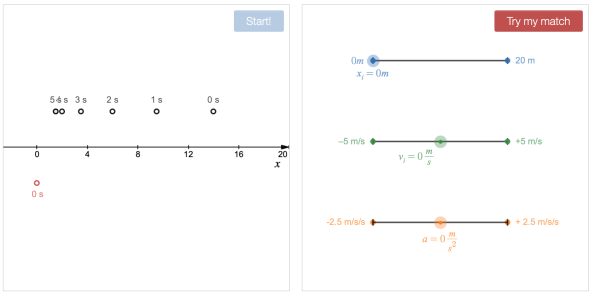
Desmos Motion Matching Game
In this game, students are shown a simulated motion that leaves the trace of motion diagram, and then they are asked to adjust the parameters of a model to match the motion.
https://teacher.desmos.com/activitybuilder/custom/5f557fa7730a5b40cc090517